How to Know Which Linear Transformation Should Use
The relationship between the variables is linear. The sensible use of linear regression on a data set requires that four assumptions about that data set be true.

Linear Transformations Video Khan Academy
Then depending on the curved pattern displayed and whether or not the origin is a data point it will allow you to select the best transformation model to achieve linearity.

. In order to call a particular function to be a linear transformation or linear map it has to satisfy the following properties math1. For example the slopes of the untransformed data are 0-790-10 -0088 and -2-0180-90 -0022. RnRm which is matrix-vector.
Some of the most famous statisticians of the 20th century thought a lot about this problem and well review some of their key ndings in the next sections. Exp 0198 1 100 219. For example the function is a linear transformation.
You can use a data transformation to be able to include the nonlinear relationship in a linear model. Note that a linear transformation must be between vector spaces of equal dimension in order to be invertible. A linear transformation is a function T.
Determining the right model to choose is easiest to determine after looking at a scatterplot of the data. To see why consider the linear transformation. T inputx outputx T i n p u t x o u t p u t x.
I know that no two elements of the image will be the same with those 3 vectorsbut if we take 3 other vectors that form a basis wed get another linear transformation that spans the image so it wouldnt be unique I would think. Similar to determining if a subset of vectors is a subspace there are 3 conditions that have to be met if a transformation is to be linear. It takes an input a number x and gives us an ouput for that number.
If this is a linear transformation then this should be equal to c times the transformation of a. But how should we proceed. This transformation will create an approximate linear relationship provided the slope between the first two points equals the slope between the second pair.
T u v T u T v - Addition in V to addition in W. A Linear Transformation is just a function a function f x f x. Or with vector coordinates as input and the corresponding vector coordinates output.
We know that if the data are nonlinear we will need to apply a nonlinear transformation to X andor Y in order to straighten out the plot. And the second one is if I take the transformation of any scaled up version of a vector -- so let me just multiply vector a times some scalar or some real number c. To find the coefficients c 1 c 2 c 3 we consider the augmented matrix.
The coefficient is 0198. The second method is to find the linear combination. That seems pretty straightforward.
TaX aTX math T is a function X and Y are vectors and a is a scalar. We transform the response y values only. Is there an easy way to identify that a function is a linear transformation.
For the vector spaces V and W the function T. Showing a transformation is linear using the definition. In Linear Algebra though we use the letter T for transformation.
T c u c T u - Scalar multiplication in V to SM in W. But neither nor are linear transformations. We transform both the predictor x values and response y values.
Examine term of each component of. As I see it you have two basic choices. 1 2 0 x 1 3 1 y 1 5 2 z and we reduce this matrix by elementary row operations.
TXY TX TY math math2. If the substantive reasons arent met then it may be best to use a different regression method but maybe not. Such data transformations are the focus of this lesson.
My book gives an example of proving T v 1 v 2 v 1 v 2 v 1 2 v 2 is a linear. To introduce basic ideas behind data transformations we first consider a simple linear regression model in which. We transform the predictor x values only.
Rn Rm be a linear transformation. The general idea behind transformation is to make a variable linear. If Ais any m nmatrix then the function T.
V W is a linear transformation of V mapping into W when two properties are true for all vectors u v and any scalar c. Therefore if we have a vector v a basis in both vector spaceV W and m points with v fv pair we can determine linear transformation. For this we have to know how to transform the points into the first basis in V then calculate the matrix M and finally.
X c 1 1 1 1 c 2 2 3 5 c 3 0 1 2 and use the linearity of the linear transformation. 1 Tx y Tx Ty for all xy 2Rn 2 Tcx cTx for all x 2Rn and c2R. If each of these terms is a number times one of the components of x then f is a linear transformation.
The data is homoskedastic meaning the variance in the residuals the difference in the real and predicted values is more or less constant. Therefore you can try various transformations and test it for linearity using tests for normality as well as visual displays. Or you can use nonlinear regression and specify the nonlinear relationship for one independent variable and a linear relationship for the other independent variable.
First you can only. Weve already met examples of linear transformations. Whether you should log transform a variable depends on both statistical and substantive considerations.
Then the matrix A satisfying Tx Ax is given by A Te1 Ten where ei is the ith column of In and then Tei is the ith column of A. Lets see if we can apply these rules to figure out if some actual transformations are linear or. One question is do the relations La1 b1 Lak bk define a consistent map on U.
The transformation of a vector in one basis to other basis using the corresponding matrix of the transformation. Mathematically this means that the following two rules hold for any vectors u and v in the domain and all scalars c and d. Exponentiate the coefficient subtract one from this number and multiply by 100.
T x y z x y y z T xyz x - y y - z T x y z xy yz from. RnRm which satis es. The following Corollary is an essential result.
When we say that a transformation is linear we are saying that we can pull constants out before applying the transformation and break the transformation up over addition and subtraction. When is linear regression appropriate. RnRm is a linear transformation then T0 0.
This gives the percent increase or decrease in the response for every one-unit increase in the independent variable.

Lesson 1 Let T R3 To R2 Is It A Linear Transformation One To One And Onto Find A Youtube
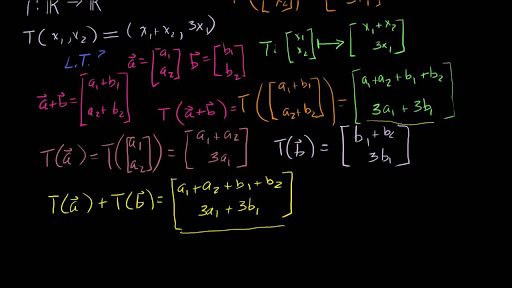
Linear Transformations Video Khan Academy

Linear Algebra Example Problems Finding A Of A Linear Transformation 2 Youtube
No comments for "How to Know Which Linear Transformation Should Use"
Post a Comment